Ryfujk

Квадрат
Правильний чотирикутник (тетрагон)
Вид	Правильний многокутник
Ребра і вершини	4
Символ Шлефлі	{4}
Діаграма Коксетера
Група симетрії[en]	Дієдральна (D4), порядок 2×4
Внутрішній кут (градуси)	90°
Властивості	опуклий, вписується в коло, рівносторонній[en], ізогональний, ізотоксальний[en]

Квадра́т — чотирикутник, у якого всі сторони рівні і всі кути прямі. Для задання квадрата необхідно і достатньо задати дві точки на координатній площині, які відповідатимуть будь-яким двом кутам та врахувати їх суміжність.

Квадрат є одночасно ромбом та прямокутником і навпаки: кожна фігура яка є одночасно ромбом та прямокутником є квадратом.

Формули, що пов'язані з квадратом |

• Чорний колір — квадрат,
• Блакитний колір: описане коло;
• Коричневий колір: вписане коло

Якщо a{displaystyle a} — довжина сторони квадрата, тоді

• 
  Площа квадрата: S=a2{displaystyle S=a^{2}}
  


• Довжина діагоналі: d=a2{displaystyle d=a{sqrt {2}}}
  


• 
  Радіус вписаного кола: r=a2{displaystyle r={frac {a}{2}}}
  


• 
  Радіус описаного кола: R=22a{displaystyle R={frac {sqrt {2}}{2}}a}
  


• 
  Периметр квадрата: P=4a=42R=8r{displaystyle P=4a=4{sqrt {2}}R=8r}
  

Властивості |

• У квадрат завжди можна вписати коло;


• Навколо квадрата завжди можна описати коло.

Як і в будь-якого опуклого чотирикутника в квадрата:

• Сума всіх внутрішніх кутів дорівнює 2π (360 градусів).

Як і в будь-якому прямокутнику:

• Протилежні сторони паралельні.


• 
  Діагоналі діляться точкою перетину навпіл.


• Точка перетину діагоналей є центром симетрії квадрата.


• Діагоналі рівні між собою.

Як і в будь-якому ромбі:

• Діагоналі є бісектрисами кутів.


• Діагоналі перетинаються під прямим кутом.


• Діагоналі є осями симетрії.

Побудова |

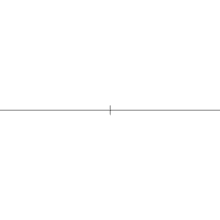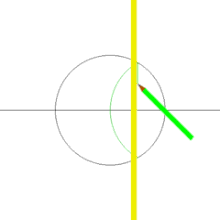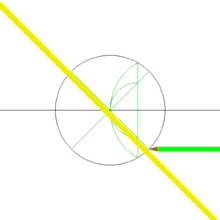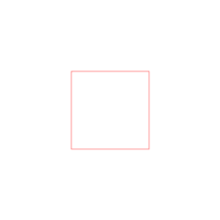
Побудова квадрата за допомогою циркуля та лінійки

Квадрат можна побудувати за допомогою циркуля та лінійки за схемою зображеною праворуч. Можна також побудувати дві перпендикулярні прямі, провести коло з центром у точці перетину прямих — чотири точки перетину прямих та кола будуть вершинами даного квадрата.

Див. також |

Вікісховище має мультимедійні дані за темою: Category:Squares (geometry)

• Ромб


• Прямокутник


• Куб


• Гіперкуб


• Магічний квадрат


• Квадратура круга


• Квадрування квадрата