Закон обернених квадратів Зміст Обґрунтування | Прояви |...
Філософія фізикиНауковий метод
Гравітаціятіловсесвітнього тяжіння1645Ісмаелем Буйо (Булліальдом)Йоганна Кеплеразаконів КеплераХристияна ГюйгенсаафеліїперигеліїРоберт ГукДжованні Альфонсо Бореллі166616701679Ісаака Ньютона"Начала"РеномГаллеємзакон КулонаВтМеркуріяВтамплітуданапруженості електричного полямагнітної індукціїрентгенографіїпроменевій терапіїпотенціального векторного полядивергенціїосвітленістьджерелом світла
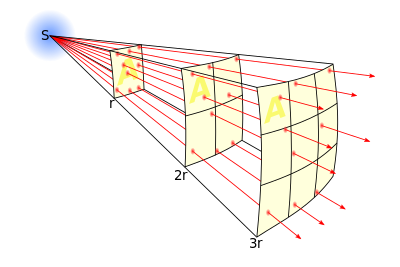
Лінії позначають потік, що випромінюється джерелом. Загальна кількість ліній потоку залежить від потужності джерела і залишається незмінною зі збільшенням відстані від нього. Збільшення щільності ліній (кількість ліній на одиницю площі) означає сильніше поле. Щільність ліній потоку обернено пропорційна квадрату відстані від джерела, оскільки площа поверхні сфери зростає пропорційно квадрату радіусу. Таким чином, сила поля обернено пропорційна квадрату відстані від джерела поля.
Закон обернених квадратів — закон, який стверджує, що значення деякої фізичної величини в даній точці простору обернено пропорційне квадрату відстані від джерела поля, яке характеризує ця фізична величина.
Зміст
1 Обґрунтування
2 Прояви
2.1 Гравітація
2.2 Електростатика
2.3 Світло та інші види електромагнітного випромінювання
3 Застосування в теорії поля
4 Примітки
5 Посилання
Обґрунтування |
Закон обернених квадратів у загальному випадку застосовується, коли лінії дії деякої сили, або енергія або інша величина, що зберігає повне значення розходиться (поширюється) в радіальному напрямку від джерела. Оскільки площа сфери (що визначається за формулою 4πr2{displaystyle 4pi r^{2}}) зростає пропорційно квадрату відстані від джерела (радіуса сфери), а випущене випромінювання віддаляється все далі від джерела, це випромінювання повинно проходити через поверхню, площа якої зростає пропорційно квадрату відстані від джерела. Отже, інтенсивність випромінювання, що проходить через одну і ту ж площу, обернено пропорційна квадрату відстані від джерела.
Прояви |
Гравітація |
Гравітація — це взаємодія між двома об'єктами, що мають масу. Такі об'єкти підпорядковуються закону всесвітнього тяжіння:
- Сили гравітаційної взаємодії між двома тілами (матеріальними точками) прямо пропорційні добутку їхніх мас, і обернено пропорційні квадрату відстані між ними. Ці сили завжди діють і спрямовані вздовж прямої, що з'єднує ці тіла (матеріальні точки).
Якщо розподіл мас в деякому матеріальному об'єкті має сферичну симетрію, то такий об'єкт може розглядатися як тіло (матеріальна точка).
Однак, якщо ми хочемо розрахувати силу взаємодії між масивними тілами, ми повинні скласти векторно сили взаємодії між усіма парами тіл, що утворюють дане масивне тіло, і отримана взаємодія може не підкорятися закону обернених квадратів. У той же час, якщо відстані між двома масивними об'єктами дуже великі в порівнянні з розмірами цих об'єктів, то доцільно розглядати ці об'єкти як матеріальні точки при розрахунку сил гравітаційної взаємодії між ними.
Як закон обернених квадратів закон всесвітнього тяжіння був сформульований 1645 року Ісмаелем Буйо (Булліальдом). Це відрізнялося від припущення Йоганна Кеплера про обернено пропорційну залежність від відстані. Але Булліальд не визнавав справедливість ні другого і третього законів Кеплера, ні рішення Християна Гюйгенса для руху по колу. Булліальд вважав, що сонце притягається в афелії і відштовхується в перигелії.
Роберт Гук і Джованні Альфонсо Бореллі 1666 року докладно описали гравітаційну силу як силу, що притягує.[1] У лекції 1670 року Гук пояснив, що гравітація властива «усім небесним тілам» і ввів принцип, який стверджує, що сила гравітації зменшується з відстанню. 1679 року Гук прийшов до висновку, що гравітація має обернену пропорційну залежність квадрату відстані. Він повідомив про це в листі до Ісаака Ньютона. Гук був досить різкий, незважаючи на те, що у своїй роботі "Начала" Ньютон визнав, що Гук поряд з Реном і Галлеєм незалежно один від одного застосовували закон обернених квадратів для сонячної системи,[2] а також віддав данину поваги Булліальду.
Електростатика |
Сила тяжіння або відштовхування, що діє між двома зарядженими частинками, не тільки прямо пропорційна добутку зарядів, а також є обернено пропорційною квадрату відстані між ними. Це твердження відоме як закон Кулона.
Світло та інші види електромагнітного випромінювання |
Інтенсивність світла (тобто, енергія, що припадає на одиницю площі в одиницю часу) або інших лінійних хвиль, що випромінюється точковим джерелом обернено пропорційна квадрату відстані від джерела. Це означає, наприклад, що об'єкт, переміщений на відстань у 2 рази більшу від джерела, отримує лише чверть тієї потужності, яку він отримував в первісному положенні.
Наприклад, інтенсивність сонячних променів становить 9140 Вт на квадратний метр на орбіті Меркурія, і лише 1370 Вт на орбіті Землі (на ту ж площу) — триразове збільшення відстані спричиняє дев'ятикратне зменшення інтенсивності сонячних променів.
На відміну від інтенсивності і від поля в статичному випадку, амплітуда напруженості електричного поля і магнітної індукції в електромагнітній хвилі від точкового джерела падає зворотно пропорційно першому степеню відстані:
- Ea,Ba∝1r.{displaystyle E_{a},B_{a}propto {1 over r}.}
Фотографи та театральні майстри по світлу використовують закон обернених квадратів для вибору оптимального місця положення освітлювальних приладів.
Закон обернених квадратів може бути застосований лише для точкових джерел світла; найбільш поширені в приміщеннях циліндричні лампи денного світла не є точковими джерелами, і тому до них не можна застосовувати закон обернених квадратів, на відміну від більшості інших джерел штучного випромінювання.
Закон обернених квадратів має деяке значення в діагностичній рентгенографії та променевій терапії для розрахунку дози опромінення. Однак ця пропорційність не дотримується в практичних випадках, незважаючи навіть на те, що розміри джерел опромінення набагато менше відстаней до об'єкта опромінення.
Формули закону обернених квадратів в рентгенографії мають вигляд:
- I1I2=(r2r1)2{displaystyle {frac {I_{1}}{I_{2}}}=left({frac {r_{2}}{r_{1}}}right)^{2}}
де
- I — інтенсивність,
- r — відстань (радіус).
Застосування в теорії поля |
Для потенціального векторного поля в тривимірному просторі закон обернених квадратів пов'язаний з властивістю дивергенції дорівнювати нулю поза джерелом.

Цей закон дозволяє визначити освітленість, що створюється в розрахунковій точці джерелом світла, що знаходиться на відстані r{displaystyle r} від цієї точки.
Eθ=Iθr2cos(θ),{displaystyle E_{theta };={frac {I_{theta }}{r^{2}cos(theta )}},}
- де Iθ;{displaystyle I_{theta };} — сила світла джерела світла (світильника)
θ;{displaystyle theta ;} — кут між напрямом випромінювання і перпендикуляром до опромінюваної поверхні.
Закон квадрата відстані застосовний, якщо відстань між джерелом світла і розрахунковою точкою, принаймні, в 5 разів більша від максимального розміру джерела (r>5l).
Примітки |
↑ Гравітація Гука ще не була універсальною, хоча вона наблизилася до загальної універсальності набагато більше, ніж попередні гіпотези: Див. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
↑ Ньютон визнавав роль Рена, Гука і Галлея в цьому зв'язку в Scholium to Proposition 4 в книзі I (у всіх виданнях): див., наприклад, англійський переклад «Начал» від 1729 року, на стр. 66.
Посилання |
Закон обернених квадратів (Анімація)(англ.)






